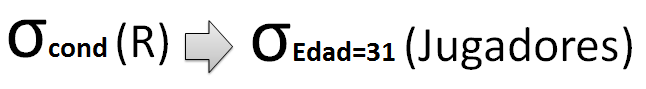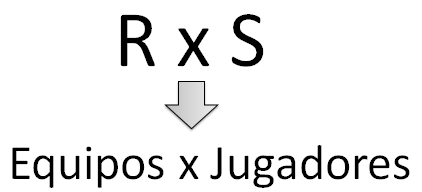Tema 6. Lenguajes Relacionales
6. Lenguajes relacionales
Los lenguajes relacionales tienen como objetivo escribir consultas para modificar o seleccionar datos de una base de datos. Los lenguajes relacionales más importantes son el cálculo, el álgebra relacional y el SQL. Los dos primeros han precedido históricamente al SQL.
Una de las ventajas del álgebra y cálculo relacionales es que se basan en la lógica y las matemáticas con lo cual cuando se obtiene una soltura sobre los mismos, la escritura de consultas puede llegar a ser igual o incluso más rápido que en SQL.
Otra de las características de estos lenguajes relacionales es su equivalencia. Una consulta escrita con un lenguaje se puede reescribir en otro obteniendo por tanto el mismo resultado.
6.1 Tipos de lenguajes relacionales.
Existen dos tipos de lenguajes para modificar y consultar una base de datos, los procedimentales y los no procedimentales.
El álgebra relacional es de tipo procedimental mientras que el cálculo relacional es de tipo declarativo (no procedimental). Eso significa que el álgebra lo que representa son las operaciones que se van a realizar sobre las tuplas para al final obtener un resultado concreto de consulta mientras que en el cálculo relacional se especifica el resultado sin concretar las operaciones que hay que realizar para llegar a él.
Las tuplas.
Una tupla es una sucesión de atributos y valores para una instancia de una relación. Lo que equivaldría a una fila de una relación o tabla.
6.2 Álgebra relacional.
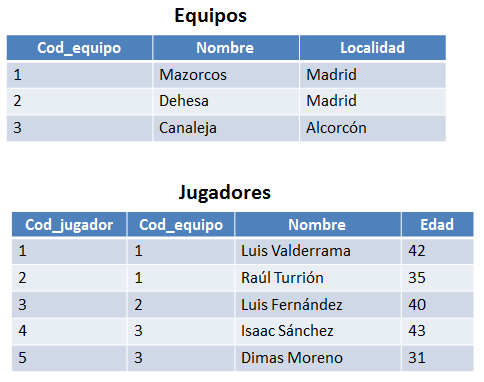
A continuación se mostrarán las tablas/relaciones con las que se van a trabajar los ejemplos de álgebra relacional:
Figura 6.1 Tablas para los ejemplos.
Se puede observar que en la relación jugadores existe una clave foránea o foreign key la cual enlaza con la relación Equipos (un jugador siempre pertenecera a un solo equipo).
6.2.1 Operaciones primitivas: selección, proyección, producto cartesiano, unión y diferencia.
Tipos de operadores.
En álgebra relacional existen operadores unarios y binarios esto significa que hay operadores que aceptan una relación y otros que necesitan dos relaciones. El resultado de cualquier operación en álgebra relacional es una nueva relación.
A continuación vamos a ver las operaciones primitivas o básicas. Con este tipo de operaciones en principio se puede realizar cualquier consulta sobre un conjunto de datos dado.
6.2.1.1 Selección
Figura 6.2 Operación de selección.
En la imagen anterior se puede observar el prototipo de una operación de selección (a la izquierda) y un ejemplo de la misma (derecha). La operación de selección permite seleccionar todas aquellas tuplas de una tabla o relación (R) siempre y cuando cumplan una condición (cond).
El resultado de ejecutar la anterior operación de selección sería el siguiente:
Figura 6.3 Resultado de la operación de selección.
6.2.1.2 Proyección
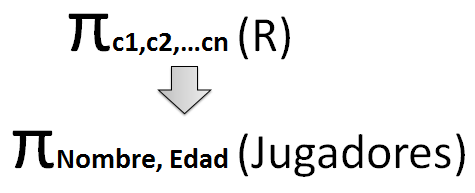
Figura 6.4 Operación de proyección.
Una proyección de una relación consiste en seleccionar un número determinado de columnas o atributos de la misma. En la figura anterior se puede ver la fórmula general y un ejemplo concreto de la misma.
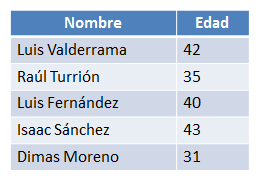
Figura 6.5 Resultado de la operación de proyección.
6.2.1.3 Producto cartesiano
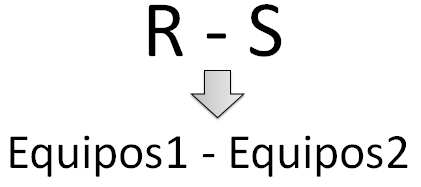
El producto cartesiano es una operación binaria y consiste en todas las tuplas de la relación R combinadas con todas y cada una de las tuplas de la relación S mostrándose los atributos de R seguidos de los atributos de S.
Figura 6.6 Operación de producto cartesiano.
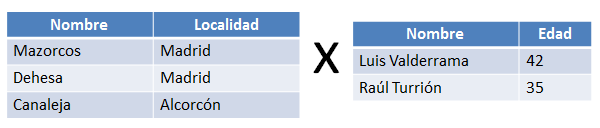
En la figura anterior se puede ver la fórmula general y un ejemplo concreto de la misma. Para que el resultado no sea tan voluminoso vamos a ver un ejemplo de producto cartesiano con una versión más reducida de las tablas equipos y jugadores.
Figura 6.7 Versión reducida de las tablas equipos y jugadores.
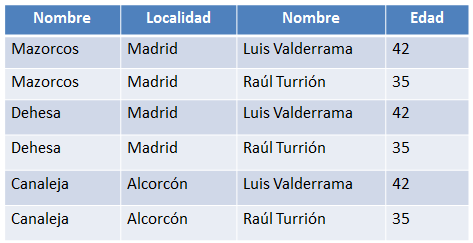
Una vez realizada la operación de producto cartesiano el resultado se puede ver en la siguiente figura:
Figura 6.8 Resultado de ejecutar el producto cartesiano de las dos relaciones anteriores.
6.2.1.4 Unión
Figura 6.9 Operación de unión.
Una operación de unión en álgebra relacional es la agrupación de dos tablas o relaciones en una nueva relación.
Con los datos que aparecen en la figura siguiente vamos a realizar una operación de unión en álgebra relacional:
Figura 6.10 Tablas con las cuales vamos a realizar la operación de unión.
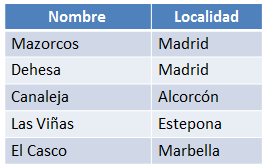
Como se explicaba anteriormente el resultado de la operación anterior será una nueva tabla con los datos de las dos anteriores. El resultado de la operación aparece en la siguiente figura.
Figura 6.11 Resultado de ejecutar la unión de las dos relaciones anteriores.
Importante en la unión y la diferencia.
Para hacer una operación de unión o diferencia ambas relaciones deben ser compatibles. Eso significa que tienen las mismas columnas.
6.2.1.5 Diferencia
Figura 6.12 Operación de diferencia.
Una operación de diferencia entre dos tablas o relaciones en álgebra relacional genera como resultado todas las tuplas de la relación R que no estén en la relación S. Veamos el resultado de una operación de diferencia con los siguientes datos:
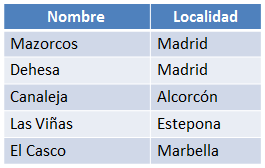
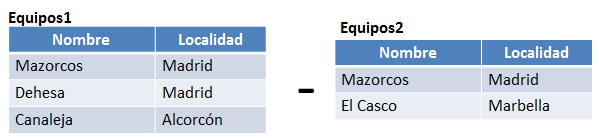
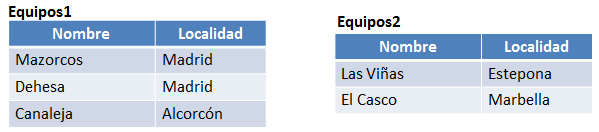
Figura 6.13 Tablas con las cuales vamos a realizar la operación de diferencia.
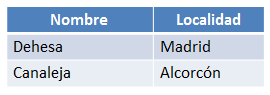
En el resultado de la operación anterior aparecerán los datos de los equipos Dehesa y Canaleja de la tabla Equipos1 pero no así el equipo Mazorcos puesto que existe en la tabla Equipos2. El resultado se puede ver en la siguiente figura:
Figura 6.14 Resultado de ejecutar la diferencia de las dos relaciones anteriores.
6.2.2 Operaciones derivadas: intersección, join y división.
Las operaciones derivadas se llaman así porque dichas operaciones se pueden realizar con una combinación de operaciones sencillas. No obstante, una operación derivada ofrece mucha más versatilidad a la hora de realizar consultas al ser estas más cortas e inteligibles.
Las operaciones derivadas en álgebra relacional más utilizadas son la intersección, join y división aunque existen otras como pueden ser la agrupación.
6.2.2.1 Intersección
Figura 6.15 Operación de intersección.
Al igual que en las operaciones de conjuntos, la intersección de dos relaciones da como resultado una nueva relación en la que aparecerán solamente los elementos que estén en ambas relaciones. Como es obvio, ambas tablas tienen que ser compatibles.
A continuación se muestran los datos de dos relaciones a las cuales se va a realizar una intersección.
Figura 6.16 Tablas con las cuales vamos a realizar la operación de intersección.
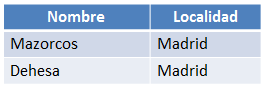
El resultado de la intersección se muestra en la figura siguiente. El único equipo que pertenece a ambas relaciones es el Mazorcos de Madrid.
Figura 6.17 Resultado de ejecutar la intersección de las dos relaciones anteriores.
6.2.2.1 Join
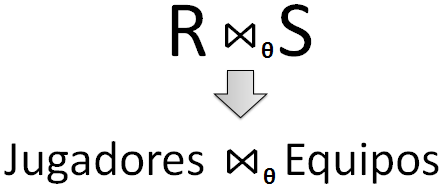
Figura 6.18 Operación de join.
La operación de join o unión natural es una de las más utilizadas cuando se va a seleccionar datos de más de una tabla. La unión natural o natural join permite reconstruir los datos de las tablas previos a la normalización.
Una unión natural equivale a realizar un producto cartesiano y una selección. En la unión natural o natural join no hace falta establecer la condición θ puesto que esta es la igualdad Clave Primaria = Clave Externa o Foránea.
En los demás join, la condición θ es libre. Generalmente esta condición implica igualdad (columna_x = columna_y) y por lo tanto se denominan equijoin aunque podrían establecerse otro tipo de condiciones como (columna_x < columna_y).
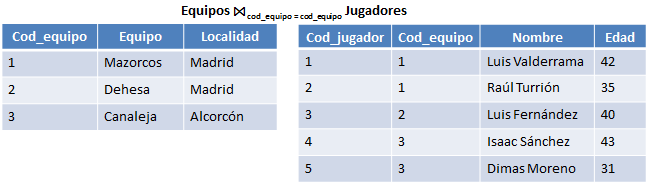
Veamos un ejemplo de realización de un join entre dos tablas:
Figura 6.19 Tablas con las cuales vamos a realizar la operación de join.
Como se ha explicado anteriormente, la condición del join cod_equipo = cod_equipo se puede obviar puesto que se ha realizado un equijoin.
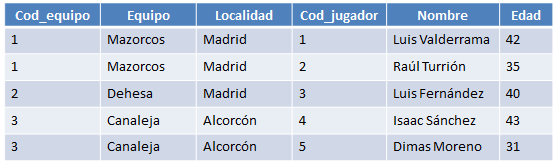
El resultado de la operación anterior se puede ver en la siguiente figura:
Figura 6.20 Resultado de ejecutar el join de las dos relaciones anteriores.
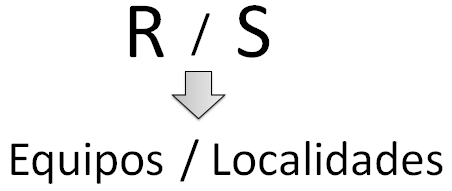
6.2.2.1 División
Figura 6.21 Operación de join.
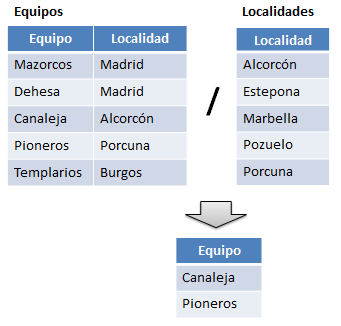
La división en álgebra relacional funciona de la siguiente manera. Imaginemos que existen dos relaciones X(a,b) e Y(b), donde a y b son columnas de dichas relaciones (en teoría pueden existir muchas columnas pero para simplificar se utilizan solo estas). La división devolverá de la relación X todos los valores de a para los cuales existe un valor de b que a su vez estará en la columna b de la relación Y.
Veamos esto con un ejemplo más visual:
Figura 6.22 Resultado de ejecutar la de división de las dos relaciones anteriores.
Como se puede observar, el resultado de la división muestra solamente la columna Equipo de la tabla Equipos y de esta columna únicamente los equipos Canaleja y Pioneros puesto que solamente los valores Alcorcón y Porcuna existen a su vez en la relación Localidades.
6.3 Cálculo relacional
Como se ha comentado el cálculo relacional indica cuál es el problema pero no cómo resolverlo. Está basado en la lógica o cálculo de predicados de primer orden.
En los inicios de las bases de datos relacionales Codd propuso ya utilizar la lógica de predicados para el manejo de consultas.
Existen dos tipos de cálculo relacional dependiendo del tipo de variables manejadas:
-
Cálculo relacional de tuplas.
-
Cálculo relacional de dominios.
Aunque el SQL está basado en álgebra relacional, utiliza aspectos del cálculo relacional de tuplas.
6.3.1 Cálculo relacional orientado a tuplas (CRT).
En cálculo relacional de tuplas las consultas a realizar a una base de datos relacional tienen la siguiente forma:
{t|F(t)}
Donde t es una tupla y F(t) es una fórmula sobre la variable tupla t.
Veamos algunos ejemplos del CRT:
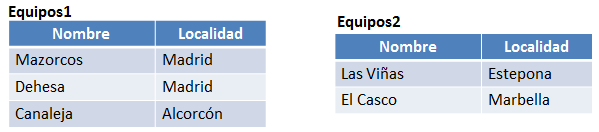
Figura 6.23 Relaciones Equipos1 y Equipos2
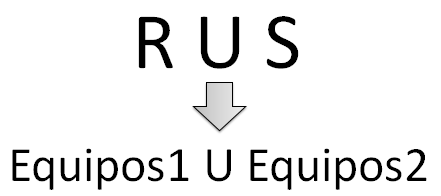
Ejemplo1: Tenemos las dos relaciones anteriores y se quiere obtener la unión o el nombre y localidad de los equipos registrados en cualquiera de las dos tablas (Equipos1 U Equipos2). La consulta en cálculo relacional de tuplas sería la siguiente:
{ t | Equipos1(t) ∨ Equipos2(t) }
El resultado de dicha consulta sería el siguiente:
Figura 6.24 Resultado de ejecutar la consulta anterior
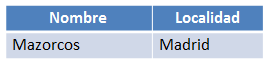
Ejemplo2: Si necesitamos conocer aquellos equipos madrileños registrados en la tabla Equipos1 la consulta sería la siguiente:
{ t | Equipos1(t) ∧ t.Localidad=’Madrid’ }
El resultado de dicha consulta sería el siguiente:
Figura 6.25 Resultado de ejecutar la consulta anterior
6.3.2 Cálculo relacional orientado a dominios (CRD).
En el cálculo relacional de dominios el funcionamiento es similar salvo que ahora se utilizan variables dominio. Las variables no representan una tupla entera sino que toman valores en el dominio de los atributos de una relación.
El formato de representación de una forma en CRD sería el siguiente:
{ a1, a2, …, ak | F(a1, a2, …, ak) }
Veamos cómo se representan los ejemplos anteriores de CRT en CRD:
Figura 6.26 Relaciones Equipos1 y Equipos2
Ejemplo1: Tenemos las dos relaciones anteriores y se quiere obtener la unión o el nombre y localidad de los equipos registrados en cualquiera de las dos tablas (Equipos1 U Equipos2). La consulta en cálculo relacional de dominios sería la siguiente:
{ Nombre,Localidad | Equipos1(Nombre,Localidad) ∨ Equipos2(Nombre,Localidad) }
Ejemplo2: Si necesitamos conocer aquellos equipos madrileños registrados en la tabla Equipos1 la consulta sería la siguiente:
{ Nombre,Localidad | Equipos1(Nombre,Localidad) ∧ Localidad=’Madrid’ }
6.4 Lenguajes comerciales: SQL (Structured Query Language), QBE (Query By Example)
Durante las décadas de los sesenta y setenta Edgar Frank Codd trabajó en lo que hoy en día ha desembocado en el modelo relacional. Fue en 1970 cuando publicó uno de sus trabajos más importantes «Un modelo relacional de datos para grandes bancos de datos compartidos» y ese fué el germen de las actuales bases de datos.
Junto con el modelo relacional propone un sublenguaje de acceso a dichos datos llamado SEQUEL (Structured English Query Language) el cual fue el predecesor del SQL (Structured Query Language).
Actualmente se utiliza la segunda versión llamada SQL2 o SQL92 la cual es un estándar revisado y ampliado del primer SQL (SQL1 o SQL86). La mayoría de los sistemas gestores de bases de datos actuales trabajan con esta versión que permite una gran variedad de operaciones aunque haya sido revisado en fechas posteriores introduciendo nuevas características o pequeñas modificaciones a las existentes.
Es un sistema de consulta como puede ser el SQL pero pretende ser más sencillo de utilizar. Fue ideado al igual que el SQL en la década de los 70 por IBM. Al principio solamente era un lenguaje de consulta de datos pero más tarde se añadieron funcionalidades para poder buscar audio, video o imágenes.
Su filosofía sigue utilizándose en muchas para la búsqueda de conceptos por ser sencillo y eficaz.
SQL tiene dos subcomponentes muy importantes como son el lenguaje de definición de datos o LDD y el lenguaje interactivo de manipulación de datos o LMD:
-
El LDD o Lenguaje de Definición de Datos tiene todo tipo de comandos para crear las estructuras y esquemas de relación, así como el borrado y la modificación de los mismos. Con el LDD entre otras operaciones podemos crear o modificar tablas que son los contenedores básicos donde se almacenan los datos en una base de datos relacional, se pueden crear relaciones entre ellas, establecer atributos de las mismas, etc, así como borrarlas. También con el LDD se podrán definir restricciones de integridad que deberán cumplir los datos alojados en dichas tablas. Otra característica de este lenguaje es que se pueden establecer derechos de acceso tanto a las relaciones como a las vistas estableciendo de ese modo el nivel de seguridad requerido.
-
Con el LMD o Lenguaje de Manejo de Datos se pueden consultar dichas estructuras y recuperar los datos según los criterios establecidos. Dicho lenguaje se basa en álgebra relacional y cálculo relacional. Su potencia y robustez reside sobre todo en la base matemática de estos dos últimos lenguajes.
-
También existe el LCD o Lenguaje de Control de Datos que permite al administrador del sistema o propietario de un objeto otorgar o quitar privilegios sobre el mismo.
En el siguiente capítulo se estudiarán en profundidad algunas de las características del lenguaje SQL.
6.4.1 Sistemas de Gestión de bases de datos con soporte SQL.
Actualmente, la mayoría de bases de datos ya sean comerciales o de software libre utilizan SQL como lenguaje de manipulación de las mismas. Las bases de datos más utilizadas en la actualidad son MySQL, Oracle y SQL Server.
Figura 6.27. Ficha de la base de datos MySQL